
An alloy system based on iron is described in which it has been possible to create a high density of interfaces by heat-treatment alone. The resulting structure consists of a mixture of slender platelets of bainitic ferrite, just 20-40 nm in thickness, embedded in a matrix of carbon-enriched austenite. The rate at which this structure evolves is slow by conventional standards, but this permits components to be made which are large in all three dimensions, with uniform properties throughout. The fundamental mechanisms behind this novel nanostructured steel are reviewed, along with the factors determining its strength, ductility and fracture toughness. It is argued that although reasonable toughness can be achieved in the context of strength levels exceeding 2000 MPa, the impact toughness remains poor and that it may not be possible to improve this particular parameter.
Proceedings of the Royal Society A, 466 (2010) 3-18.

H. K. D. H. Bhadeshia
An alloy system based on iron is described in which it has been possible to create a high density of interfaces by heat-treatment alone. The resulting structure consists of a mixture of slender platelets of bainitic ferrite, just 20-40nm in thickness, embedded in a matrix of carbon-enriched austenite. The rate at which this structure evolves is slow by conventional standards, but this permits components to be made which are large in all three dimensions, with uniform properties throughout. The fundamental mechanisms behind this novel nanostructured steel are reviewed, along with the factors determining its strength, ductility and fracture toughness. It is argued that although reasonable toughness can be achieved in the context of strength levels exceeding 2000MPa, the impact toughness remains poor and that it may not be possible to improve this particular parameter.
A nanostructured material is here defined as one containing an exceptionally large density of strong interfaces, rather than one which simply contains a minor fraction of features such as precipitates, which are small in size. The desire for such materials in the engineering context comes from the expectation of novel mechanical properties, particularly the stress that can safely be tolerated in service. It is difficult to invent such materials because any design must address three basic issues:
These are formidable challenges and the process of design can begin with a consideration of how strength can be achieved. The long-range periodicity which is assumed to typify the crystalline state is in practice punctuated by defects, some of which make a significant contribution to configurational entropy and hence can exist in thermodynamic equilibrium. This kind of entropy scales with the number of entities (atoms) in the crystal and hence it is only possible to approximate perfection in small crystals (Gorsuch, 1959). Such crystals can be strong because in the absence of defects, deformation must occur by the wholesale glide of planes over each other, rather than by the propagation of discontinuities such as dislocations. Micrometer sized crystals of pure iron have achieved strength levels in excess of 10 GPa (Brenner, 1956; Sears et al., 1954), although in principle the strength can exceed 20 GPa (Clatterbuck et al., 2002). The crystals becomes weaker as they are made larger, both because of the thermodynamically stabilised defects and also accidents of growth. This is fundamentally why the impressive mechanical properties of carbon nanotubes are not maintained (and indeed, should not be expected to be maintained) when the tubes become long (Pugno, 2007b; Bhadeshia, 2005b; Pugno, 2007a; Ruoff, 2006).
An alternative method for manufacturing sizeable strong materials is to introduce large numbers of defects such as interfaces or dislocations, which interfere with the ordinary mechanisms of slip or twinning. The defects can be introduced by deformation. Techniques which involve severe plastic deformation are limited in the shape of the final product and in the quantity that can be produced at reasonable cost. Examples include fine nanostructured-wire with a strength in excess of 5 GPa (Bhadeshia and Harada, 1993); metals subjected to equal-channel angular extrusion in which redundant work is used in order to achieve large plastic strains whilst maintaining the external shape of the object being deformed (Segal, 1999; Segal, 2002; Horita et al., 2000). Accumulative roll-bonding involves the repeated rolling and folding of sheet material in order to accomplish strain increments without thinning the sample entering the rolls; the process is suited for large scale production but does not lead to particularly fine grains, which tend to be closer to micrometers than nanometers in size (Saito et al., 1998).
Thermomechanical processing (Speich et al., 1984) is particularly suited to the large scale production of fine-grained steels by phase transformation from the deformed parent austenite. However, the minimum ferrite grain size achieved in practice is about 1![]() m, partly because the speed of production and the thickness of the steel leads to recalescence during transformation, and hence prevents the achievement of the large undercoolings needed to refine the grain size (Yokota et al., 2004).
m, partly because the speed of production and the thickness of the steel leads to recalescence during transformation, and hence prevents the achievement of the large undercoolings needed to refine the grain size (Yokota et al., 2004).
There are a couple of further difficulties. The ductility decreases sharply as the grain size in a polycrystalline metal is reduced (Howe, 2009; Howe, 2000). Secondly, there is often a requirement for rapid heat-treatment which becomes impractical for large components.
A recent development seems to avoid all of these difficulties, and meets the criteria outlined in the opening paragraph of this paper. A nanostructure has been achieved in large lumps of steel by phase transformation, with the design of the steel based on an understanding of the atomic mechanisms of crystal growth in the solid state (Caballero et al., 2002; Caballero et al., 2001b; Caballero et al., 2001a; Garcia-Mateo et al., 2003b). Commercial applications of the steel have been described previously and are not repeated here (Caballero and Bhadeshia, 2004).
Strong steels can be produced by martensitic transformation but this requires rapid cooling unless use is made of sufficient quantities of expensive alloying elements. The bainite reaction has a comparatively greater capacity for control; its structure can be generated by isothermal or continuous cooling transformation.
There are many features of the atomic mechanism of the bainite reaction which are not yet understood (Bhadeshia, 1999), but as demonstrated in a recent compendium![]() , there has been sufficient progress to enable the quantitative design of useful steels. Bainite as a phase mixture has been known since the 1930s, but the scale of the structure in ordinary steels is in the micrometer range. It is however known that the structure can be refined by reducing the transformation temperature (Singh and Bhadeshia, 1998). It is of interest therefore, to investigate the lowest temperature at which bainite can form, whilst avoiding martensitic transformation.
, there has been sufficient progress to enable the quantitative design of useful steels. Bainite as a phase mixture has been known since the 1930s, but the scale of the structure in ordinary steels is in the micrometer range. It is however known that the structure can be refined by reducing the transformation temperature (Singh and Bhadeshia, 1998). It is of interest therefore, to investigate the lowest temperature at which bainite can form, whilst avoiding martensitic transformation.
The highest temperature at which bainite can form in a steel of given composition is known as the bainite-start temperature (![]() ), and the martensite-start temperature (
), and the martensite-start temperature (![]() ) is similarly defined. The theory determining these start-temperatures has been described elsewhere (Kaufman and Cohen, 1958; Ghosh and Olson, 2001; Bhadeshia, 1981b) but it is summarised here after defining some thermodynamic quantities. The chemical free energy change accompanying the diffusionless growth of either bainite or martensite when neglecting all the stored energy terms is written
) is similarly defined. The theory determining these start-temperatures has been described elsewhere (Kaufman and Cohen, 1958; Ghosh and Olson, 2001; Bhadeshia, 1981b) but it is summarised here after defining some thermodynamic quantities. The chemical free energy change accompanying the diffusionless growth of either bainite or martensite when neglecting all the stored energy terms is written
![]() , where
, where ![]() represents the Gibbs free energy and
represents the Gibbs free energy and ![]() and
and ![]() represent the product and parent phases respectively. However, these are not equilibrium transformations and there is energy stored inside the steel, for example in the form of elastic strains, that must be accounted for; in the case of bainite this is written
represent the product and parent phases respectively. However, these are not equilibrium transformations and there is energy stored inside the steel, for example in the form of elastic strains, that must be accounted for; in the case of bainite this is written
![]() (Bhadeshia and Edmonds, 1980).
(Bhadeshia and Edmonds, 1980).
The nucleation stage of bainite involves the partitioning of carbon so the chemical free energy change (
![]() ) for this stage is larger; the magnitude of this driving force must exceed a value prescribed by a function
) for this stage is larger; the magnitude of this driving force must exceed a value prescribed by a function
![]() in order to obtain a detectable nucleation rate (Bhadeshia, 1981b).
in order to obtain a detectable nucleation rate (Bhadeshia, 1981b). ![]() is defined when both the nucleation and growth conditions are satisfied simultaneously:
is defined when both the nucleation and growth conditions are satisfied simultaneously:
|
(a)
![\includegraphics[width=0.45\textwidth]{Figure1a.eps}](./review/img20.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Figure1b.eps}](./review/img21.png)
|
Martensitic transformation occurs when
![]() becomes less than a critical value
becomes less than a critical value
![]() given by the function
given by the function
![]() :
:
Suppose we now use this theory to estimate the lowest temperature at which bainite can form. Such calculations are illustrated in Fig. 1a, which shows for an example steel, how the ![]() and
and ![]() temperatures vary as a function of the carbon concentration. There appears to be no lower limit to the temperature at which bainite can be generated. On the other hand, the rate at which bainite forms slows down dramatically as the transformation temperature is reduced, Fig. 1b. It may take hundreds or thousands of years to generate bainite at room temperature. For practical purposes, a transformation time of tens of days is reasonable, corresponding to a carbon concentration of about 1 wt%, in which case bainite can be generated at a temperature as low as 125
temperatures vary as a function of the carbon concentration. There appears to be no lower limit to the temperature at which bainite can be generated. On the other hand, the rate at which bainite forms slows down dramatically as the transformation temperature is reduced, Fig. 1b. It may take hundreds or thousands of years to generate bainite at room temperature. For practical purposes, a transformation time of tens of days is reasonable, corresponding to a carbon concentration of about 1 wt%, in which case bainite can be generated at a temperature as low as 125![]() C, which is so low that the diffusion distance of an iron atom is an inconceivable 10
C, which is so low that the diffusion distance of an iron atom is an inconceivable 10![]() m over the time scale of the experiment!
m over the time scale of the experiment!
![\includegraphics[width=11cm]{Figure2b.eps}](./review/img27.png)
|
A steel designed on this basis was manufactured and characterised (Caballero et al., 2002; Garcia-Mateo et al., 2003c; Garcia-Mateo et al., 2003b); Fig. 2 shows the structure obtained following isothermal transformation at 200![]() C, consisting of platelets of bainitic ferrite only 200-400 Å thick, with intervening regions of the parent austenite
C, consisting of platelets of bainitic ferrite only 200-400 Å thick, with intervening regions of the parent austenite ![]() . This retained austenite is important because when it undergoes stress or strain-induced martensitic transformation, it enhances the work-hardening capacity of the material, thereby avoiding the usual problem of fine-grained metals where ductility diminishes as the grain size is reduced.
. This retained austenite is important because when it undergoes stress or strain-induced martensitic transformation, it enhances the work-hardening capacity of the material, thereby avoiding the usual problem of fine-grained metals where ductility diminishes as the grain size is reduced.
Since the original work, many variations of the alloy have been studied and the structure has been characterised, both chemically and spatially to an atomic resolution. As expected from a displacive transformation mechanism in which the change in crystal structure is achieved by a deformation, there is no redistribution of substitutional atoms on the finest conceivable scale (Peet et al., 2004a; Caballero et al., 2007). The carbon concentration in the retained austenite can be as high as 5-7 at.%, depending on the transformation conditions (Bruna et al., 2005). In situ observations indicate that the carbon concentration in the austenite becomes heterogeneously distributed once it begins to transform into bainitic ferrite (Stone et al., 2008) because a greater quantity of carbon is trapped in the films of retained austenite enclosed by platelets of bainitic ferrite, than within the larger blocks that persist between different crystallographic variants of bainite. As a result, two separable peaks are observed associated with each austenite reflection in synchrotron X-ray diffraction experiments as transformation evolves (Fig. 3). Similar observations have previously been reported on ordinary bainitic steels (Matas and Hehemann, 1961; Le-Houillier et al., 1971; Bhadeshia and Waugh, 1982). It should be emphasised that an earlier synchrotron X-ray study (Babu et al., 2005) claiming that austenite evolves into regions with different lattice parameters prior to transformation was erroneous, based on artefacts in the analysis of low resolution data (Stone et al., 2008).
![\includegraphics[width=0.9\textwidth]{Waterfall.eps}](./review/img29.png)
|
The orientation relationship between the bainitic ferrite and austenite is found to be irrational, with the closely packed planes
![]()
![]() from (101)
from (101)![]() and the corresponding close-packed directions
and the corresponding close-packed directions
![]()
![]() from
from
![]() (Zhang and Kelly, 2006)
(Zhang and Kelly, 2006)![]() . Furthermore, the response of the structure as it evolves, to externally applied stress and plastic strain (Shirzadi et al., 2009; Kundu et al., 2007), is found to be predictable using the crystallographic theory of displacive transformations (Patel and Cohen, 1953; Wechsler et al., 1953; Bowles and MacKenzie, 1954). There is limited work to suggest that in these nanostructured steels, the number of different crystallographic variants of bainite that form in any given austenite grain increases as the transformation temperature is reduced (Beladi et al., 2009); however, the conclusion reached in the same work regarding the existence of the Nishiyama-Wasserman
. Furthermore, the response of the structure as it evolves, to externally applied stress and plastic strain (Shirzadi et al., 2009; Kundu et al., 2007), is found to be predictable using the crystallographic theory of displacive transformations (Patel and Cohen, 1953; Wechsler et al., 1953; Bowles and MacKenzie, 1954). There is limited work to suggest that in these nanostructured steels, the number of different crystallographic variants of bainite that form in any given austenite grain increases as the transformation temperature is reduced (Beladi et al., 2009); however, the conclusion reached in the same work regarding the existence of the Nishiyama-Wasserman
![]() orientation is unlikely to be justified by the accuracy of the crystallographic technique used. In general, the orientation relationship between austenite and bainitic ferrite must be irrational and will therefore lead to 24 possible crystallographic variants per grain of austenite, unlike the 12 associated with the Nishiyama-Wasserman relation.
orientation is unlikely to be justified by the accuracy of the crystallographic technique used. In general, the orientation relationship between austenite and bainitic ferrite must be irrational and will therefore lead to 24 possible crystallographic variants per grain of austenite, unlike the 12 associated with the Nishiyama-Wasserman relation.
The bainite obtained by low-temperature transformation is harder than ever achieved, with values in excess of 700 HV. Some strength, ductility and toughness data are illustrated in Fig. 4. The simple heat treatment involves the austenitisation of a chunk of steel (at say 950![]() C), followed by a gentle transfer into an oven at the low temperature (say 200
C), followed by a gentle transfer into an oven at the low temperature (say 200![]() C) to be held there for ten days or so. There is no rapid cooling - residual stresses are avoided. The size of the sample can be large because the time taken to reach 200
C) to be held there for ten days or so. There is no rapid cooling - residual stresses are avoided. The size of the sample can be large because the time taken to reach 200![]() C from the austenitisation temperature is much less than that required to initiate bainite. This is an important commercial advantage.
C from the austenitisation temperature is much less than that required to initiate bainite. This is an important commercial advantage.
|
(a)
![\includegraphics[width=0.42\textwidth]{strength.eps}](./review/img37.png) (b) (b) ![\includegraphics[width=0.42\textwidth]{ductility_toughness.eps}](./review/img38.png)
|
Much of the strength and hardness of the structure comes from the incredibly thin platelets of bainitic ferrite. For a true thickness ![]() , the mean lineal intercept
, the mean lineal intercept
![]() (Mack, 1956; Bhadeshia, 1997); the resulting strengthening is given by
(Mack, 1956; Bhadeshia, 1997); the resulting strengthening is given by
![]() MPa where
MPa where
![]() is in micrometers (Langford and Cohen, 1970; Langford and Cohen, 1969). The inverse dependence on
is in micrometers (Langford and Cohen, 1970; Langford and Cohen, 1969). The inverse dependence on
![]() , which does not follow the Hall-Petch relation, is because the transmission of slip across boundaries is determined by the energy required to expand dislocation loops rather than by the pile-up of the dislocations obstructed by boundaires (Langford and Cohen, 1970). With
, which does not follow the Hall-Petch relation, is because the transmission of slip across boundaries is determined by the energy required to expand dislocation loops rather than by the pile-up of the dislocations obstructed by boundaires (Langford and Cohen, 1970). With
![]() nm,
nm,
![]() MPa, which decreases to 311MPa for
MPa, which decreases to 311MPa for
![]() MPa. Fig. 4a illustrates the strength plotted as a function of the volume fraction of bainitic ferrite, against which the strength scales linearly (Bhadeshia and Edmonds, 1983), and
MPa. Fig. 4a illustrates the strength plotted as a function of the volume fraction of bainitic ferrite, against which the strength scales linearly (Bhadeshia and Edmonds, 1983), and ![]() . The inverse dependence of hardness on plate thickness is also evident in Fig. 5.
. The inverse dependence of hardness on plate thickness is also evident in Fig. 5.
The residue of strength after accounting for the plate thickness comes from dislocation forests, the intrinsic strength of the iron lattice and solution strengthening. It has long been known, using atom-probe field-ion microscopy, that bainitic ferrite contains much more carbon than is consistent with equilibrium or paraequilibrium (Bhadeshia and Waugh, 1982). It is likely that much of this excess carbon is trapped at the dislocations (Caballero et al., 2008; Zhang and Kelly, 1998; Peet et al., 2004a; Peet et al., 2004b; Bhadeshia and Waugh, 1982) created during the growth of the bainite (Swallow and Bhadeshia, 1996). There are now direct observations of the carbon at dislocations in the low-temperature bainitic ferrite (Caballero et al., 2007). The strengthening contributions of the carbon and dislocations cannot therefore be independently calculated, but are small in comparison with that due to plate size. This is why the hardness of the nanostructure is insensitive to tempering, until the onset of plate coarsening at temperatures in excess of 500![]() C (Peet et al., 2004b).
C (Peet et al., 2004b).
![\includegraphics[width=0.8\textwidth]{hardness_thickness.eps}](./review/img46.png)
|
Fig. 6 shows typical true-stress versus true-strain curves; the gradual yielding is characteristic of composite structures containing a large number density of dislocations, and may also be attributed to the transformation of some austenite during the application of stress. It is intriguing that the elongation increases as the nanostructure is generated at the higher temperature. This is in fact a general observation in these steels, and might be an outcome of the lower strength obtained following transformation at high temperatures. However, in this instance, the correlation of ductility with strength is not sensible in a statistical sense, because there are similar low-carbon, low-strength steels which do not show the high ductility illustrated in Fig. 6, for example, Parker (1977); Wang et al. (2009b); Caballero et al. (2001a); Caballero et al. (2001b); Wang et al. (2009a); Putatunda et al. (2009). The explanation seems to lie in the stress and strain-induced martensitic transformation of the retained austenite during tensile testing. The decomposition of the austenite in this manner has been calculated and measured for a variety of combinations of bainitic ferrite and austenite (Sherif et al., 2004). Fig. 7 shows the expected variation in the austenite content ![]() with strain for three cases (Bhadeshia, 2008) with the points identifying the failure strain. It is noticeable that fracture occurs when
with strain for three cases (Bhadeshia, 2008) with the points identifying the failure strain. It is noticeable that fracture occurs when
![]() . An experimental in situ study using neutron diffraction during the tensile test by Sherif (2005) concurs with this conclusion.
. An experimental in situ study using neutron diffraction during the tensile test by Sherif (2005) concurs with this conclusion.
![\includegraphics[width=0.8\textwidth]{true_stress.eps}](./review/img49.png)
|
It has been suggested that failure occurs when the austenite, which is the toughest of all the phases present, becomes geometrically isolated, i.e., it loses percolation (Bhadeshia, 2008). Garboczi et al. (1995) have modelled the percolation threshold for ellipsoidal objects placed in a matrix. Assuming the austenite is subdivided into the form of plates by the bainite, it can be represented by oblate ellipsoids with an aspect ratio ![]() of between about 1/10 and 1/100. The percolation threshold is then found to be
of between about 1/10 and 1/100. The percolation threshold is then found to be
![]() , i.e.,
, i.e.,
![]() . This is consistent with the observation that tensile failure occurs when
. This is consistent with the observation that tensile failure occurs when
![]() .
.
Fig. 7 indicates that substantial quantities of brittle martensite which forms during deformation can exist in the microstructure before failure occurs. This is because the tendency of the martensite to crack under stress depends on its absolute size, with coarse regions being most susceptible (Chatterjee and Bhadeshia, 2006). It is the fine scale of the retained austenite that permits the martensite that forms during deformation to be tolerated without compromising the ductility until the percolation threshold is reached.
Finally, some very high fracture strains and strengths have been reported for nanostructured bainite (Soliman and Palkowski, 2007), but these were measured in compression whereas all the other values reported here are for the more demanding tensile tests.
Although the occurrence of high-carbon, untempered martensite causes failure only when the percolation threshold is reached, its presence must influence the toughness. We have already seen that the fracture toughness as measured using ![]() is reasonably high, but the Charpy impact properties of these nanostructured steels are poor, with only about 5 J of impact energy absorbed at room temperature. This must be attributed to the fracture of martensite at the high strain rates associated with the impact test. It seems likely that the poor Charpy impact toughness is an intrinsic characteristic of steels containing brittle martensite in microstructures where softer phases that can accommodate the imposed strain rate are absent. After all, much greater absorbed energies are obtained in the similarly strong Aermet 100 steel where the martensite is toughened by severe tempering (Novotny, 1992).
is reasonably high, but the Charpy impact properties of these nanostructured steels are poor, with only about 5 J of impact energy absorbed at room temperature. This must be attributed to the fracture of martensite at the high strain rates associated with the impact test. It seems likely that the poor Charpy impact toughness is an intrinsic characteristic of steels containing brittle martensite in microstructures where softer phases that can accommodate the imposed strain rate are absent. After all, much greater absorbed energies are obtained in the similarly strong Aermet 100 steel where the martensite is toughened by severe tempering (Novotny, 1992).
![\includegraphics[width=10cm]{retainedaustenite.eps}](./review/img53.png)
|
The low-temperature reaction can take between 2-60 days over the range 125-325![]() C. When combined with the inherent ability of the steel to resist pearlite formation during cooling, this means that a large steel component can be cooled slowly to
C. When combined with the inherent ability of the steel to resist pearlite formation during cooling, this means that a large steel component can be cooled slowly to ![]() , thus achieving a homogeneous temperature before transformation begins. This encourages the development of uniform properties and should help avoid the development of residual stresses and hence to minimise distortion.
, thus achieving a homogeneous temperature before transformation begins. This encourages the development of uniform properties and should help avoid the development of residual stresses and hence to minimise distortion.
A transformation that can be completed within minutes or hours would nevertheless be useful when dealing with small components. The difference in free energy between austenite and ferrite (
![]() ) is the driving force for transformation. Both the nucleation and growths rate can be expected to increase as a function of
) is the driving force for transformation. Both the nucleation and growths rate can be expected to increase as a function of
![]() . The addition of cobalt and aluminium boosts
. The addition of cobalt and aluminium boosts
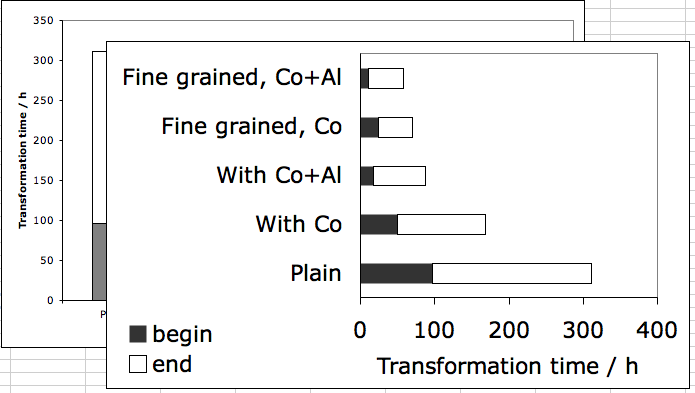
![]() , causing the rate of transformation to increase (Kinsman and Aaronson, 1973; Aaronson et al., 1966), as illustrated in Fig. 8.
, causing the rate of transformation to increase (Kinsman and Aaronson, 1973; Aaronson et al., 1966), as illustrated in Fig. 8.
![\includegraphics[width=12cm]{times.eps}](./review/img55.png)
|
There have been suggestions that the rate of transformation can be accelerated by cycling the supercooled austenite within the range ![]() to
to ![]() (Sista et al., 2007). Single step-changes in the temperature during the course of the reaction have previously been investigated (Goodenow et al., 1969), which indicated that the stresses generated by phase transformation at low temperatures can stimulate that at higher temperatures. However, detailed experiments have failed to confirm the acceleration potential of cyclic transformation when an appropriate comparison is made against the limiting isothermal transformation behaviours (Hasan et al., 2009). The original work does not seem to take account of the excursions of temperature associated with cyclic transformation. Fig. 9 shows that the `curve' associated with the cyclic transformation falls between the high and low-temperature isothermal transformation data.
(Sista et al., 2007). Single step-changes in the temperature during the course of the reaction have previously been investigated (Goodenow et al., 1969), which indicated that the stresses generated by phase transformation at low temperatures can stimulate that at higher temperatures. However, detailed experiments have failed to confirm the acceleration potential of cyclic transformation when an appropriate comparison is made against the limiting isothermal transformation behaviours (Hasan et al., 2009). The original work does not seem to take account of the excursions of temperature associated with cyclic transformation. Fig. 9 shows that the `curve' associated with the cyclic transformation falls between the high and low-temperature isothermal transformation data.
![\includegraphics[width=8cm]{7.eps}](./review/img56.png)
|
Untempered high-carbon martensitic steels can achieve a maximum hardness of about 800 HV (Bhadeshia and Edmonds, 1983) but the dissolved carbon tends to make the martensite extremely brittle. One solution is to use a low-carbon steel but to diffuse a larger concentration into the surface which is then transformed into hard martensite, in a process known as case-hardening. This typically gives a wear-resistant layer with a hardness of about 750 HV (Epshtein and Paisov, 1965), but the surface itself remains relatively brittle. Hardness approaching this level can now be achieved by the nanostructured bainite which has the additional advantage of toughness (Garcia-Mateo et al., 2003b). Case-carburised steel isothermally transformed at 200![]() C has been shown to lead to extremely fine and hard bainite (620 HV) in the surface layer, with the transformation inducing a compressive stress of about 200MPa into the surface (Zhang et al., 2008). Similar results have been claimed for bainitic cases produced at higher temperatures; it seems that the distortion associated with the production of the bainitic case is smaller than with the martensitic variety because of the less dramatic quench to the isothermal transformation temperature (Heuer et al., 2009).
C has been shown to lead to extremely fine and hard bainite (620 HV) in the surface layer, with the transformation inducing a compressive stress of about 200MPa into the surface (Zhang et al., 2008). Similar results have been claimed for bainitic cases produced at higher temperatures; it seems that the distortion associated with the production of the bainitic case is smaller than with the martensitic variety because of the less dramatic quench to the isothermal transformation temperature (Heuer et al., 2009).
The dry sliding-friction wear resistance of nanostructured bainite has been studied by Wang et al. (2008) who found that the austenite in the vicinity of the friction surface decomposes under the influence of shear strain, resulting in the formation of an even finer structure with grains of ferrite only a few nanometers in size. It was suggested that these events play a role in determining the wear resistance, which is comparable to that of quenched and tempered martensitic structures. This augers well for the development of case-hardening technology based on the nanostructured bainite.
It is interesting that transmission electron microscopy in the work by Zhang et al. (2008) revealed that the bainite was free from carbides in spite of the fact that the silicon concentration of the steel was less than 0.6 wt%. Larger concentrations of silicon have been used in all of the steels developed to generate nanostructured bainite, in order to prevent the precipitation of cementite during the course of transformation. It may be possible to use lower concentration and yet maintain a carbide-free phase mixture.
Structural steels often need to be joined by welding, which involves the local application of a heat source. The diffusion of this heat into the adjacent material causes metallurgical changes which can lead to the formation of brittle martensite when the carbon concentration of the steel is high enough, as is the case with the nanostructured bainitic steels described here.
The principal reason for the fine scale of the bainitic structure is the low transformation temperature made possible by the ![]() 1wt% of carbon. It is feasible that
1wt% of carbon. It is feasible that ![]() can also be suppressed by using large concentrations of substitutional solutes, such as nickel, in order to minimise the concentration of carbon. Unfortunately, theory indicates that the level of substitutional solute required would prevent completely the formation of bainite because the difference between the bainite and martensite-start temperatures then vanishes (Bhadeshia, 2005a). There is another difficulty discovered experimentally (Yang and Bhadeshia, 2008), that at low carbon concentrations, the thin platelets of bainite that do form tend to coalesce into coarse grains which are detrimental to toughness (Pak et al., 2008; Keehan et al., 2006). The prospects therefore do not look promising for the design of a low-carbon nanostructured bainite.
can also be suppressed by using large concentrations of substitutional solutes, such as nickel, in order to minimise the concentration of carbon. Unfortunately, theory indicates that the level of substitutional solute required would prevent completely the formation of bainite because the difference between the bainite and martensite-start temperatures then vanishes (Bhadeshia, 2005a). There is another difficulty discovered experimentally (Yang and Bhadeshia, 2008), that at low carbon concentrations, the thin platelets of bainite that do form tend to coalesce into coarse grains which are detrimental to toughness (Pak et al., 2008; Keehan et al., 2006). The prospects therefore do not look promising for the design of a low-carbon nanostructured bainite.
Considerable progress has been made in revealing the mechanism by which nanostructured bainite and its mechanical properties evolve, and in the application of this knowledge towards better design. The steel with this structure can be strong, hard, ductile and reasonably tough. However, because of its high carbon concentration, it is unlikely to be readily weldable. Furthermore, the stress or strain-induced formation of brittle martensite may make it impossible to achieve a large impact toughness. Applications of the concept have to bear these factors in mind. The exciting outcome is that for the first time, it is possible to obtain a bulk steel containing an extraordinarily high density of ferrite/austenite interfaces, at a cost which is ordinary, and which can be made in large quantities. Samples of the alloy can be simultaneously large in all three dimensions.
It is quite likely, given the level of worldwide activity in this field, that the approach used for the design of the nanostructured bainite will lead to another class of steels with a wider range of properties and a greater potential for applications. Indeed, it is encouraging that different procedures of design are also being adopted, for example, the work by Kundu et al. (2009), where artificial neural networks have been used to design and manufacture the fine bainite by transforming at the significantly higher temperature of 300![]() C in a matter of hours rather than days, without using expensive alloying elements.
C in a matter of hours rather than days, without using expensive alloying elements.
I am grateful to Professor Lindsay Greer for the provision of laboratory facilities at the University of Cambridge.
| PT Group Home | Materials Algorithms |