Computing the energy of infinite arrays of point charges, interacting with each other through Coulomb’s potential, is a central task in materials modelling. Typically, modern implementations of Ewald's method, which splits the problem into two separately convergent sums; one in real space and the other in reciprocal space, are used to do this.

Density functional theorybased electronic structure methods (such as CASTEP) require the evaluation of the ion-ion repulsive energy, neutralised by a uniform background charge. In this article a purely real-space approach is described which is straightforward to implement, and computationally efficient. It offers linear scaling and when applied to the evaluation of the electrostatic energy of neutral ionic crystals, it is shown to be closely related to the well known method due to Wolf and co-workers.

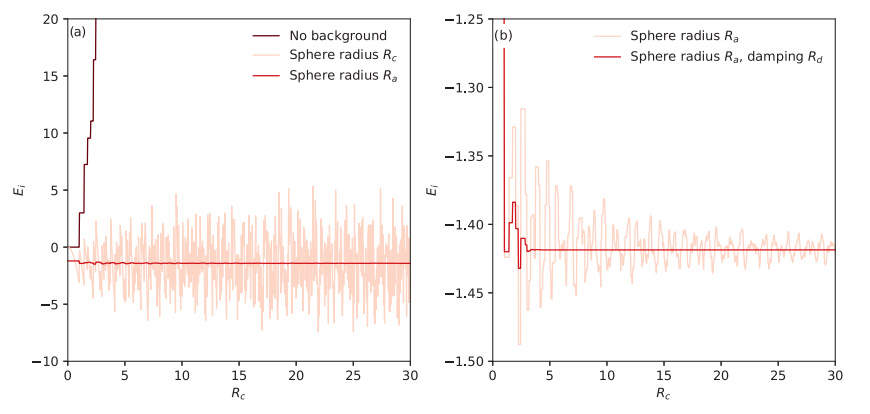
Figure: a) With no neutralising background the electrostatic sum of an array of positive charges diverges with increasing cutoff sphere radius (R_c). Adding a neutralising background sphere with the same radius stops the sum increasing, but the result oscillates strongly. Choosing a radius (R_a), which adapted so as to enforce charge neutrality, ensures convergence. b) Smearing (or damping) the charge density due to the array of charges a little leads to very accurate sums.