Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Introduction to Mechanical Properties of Materials Relation between Young's modulus and shear modulus
Introduction to Mechanical Properties of Materials AimsBefore you startIntroductionTensile test: force and extensionStress, strain and Poisson's ratioElastic deformation: Hooke's law and stiffnessViscoelasticityPlastic deformation: strength and ductilitySlip: resolved shear stress and Schmid factor, Taylor factorHardness and work hardeningCreepFracture: toughnessDuctile-brittle transition temperatureSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Relation between Young's modulus and shear modulus

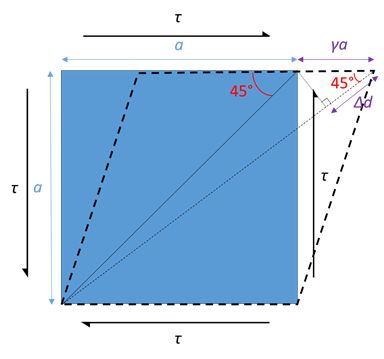
stress and strain on a cube

Consider a stress state above acting on a cube of length \( a \). Assume the shear strain \( \gamma \) is small such that the angle between the diagonal and length is approximately the same, i.e. 45°, before and after shearing.

Strain on the diagonal is

\[ \frac{{{\rm{\Delta }}d}}{{\sqrt 2 a}} = \frac{{\gamma a\;{\rm{cos}}45^\circ }}{{\sqrt 2 a}} = \frac{\gamma }{2} \]

From the definition of shear modulus,

\[ G = \frac{\tau }{\gamma } \]

Strain on the diagonal therefore is \( \frac{\tau }{{2G}} \).

Now consider a set of stress state equivalent to the above case.

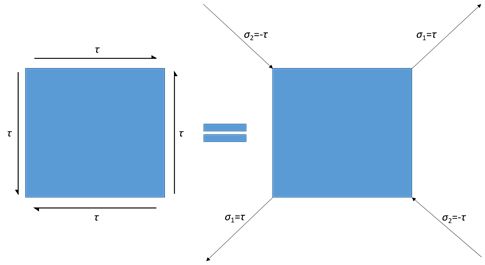
stress state

By the principle of superposition of two stress pairs, strain on the diagonal is

\[ \frac{{{\sigma _1}}}{E} - \nu \frac{{{\sigma _2}}}{E} = \frac{\tau }{E} - \nu \frac{{ - \tau }}{E} = \frac{\tau }{E}\left( {1 + \nu } \right) \]

where \( E \) is Young’s modulus and \( \nu \) is Poisson’s ratio.

Equating the diagonal strain in two cases gives the relation between Young’s modulus E and shear modulus G:

\[ \frac{\tau }{{2G}} = \frac{\tau }{E}\left( {1 + \nu } \right) \]

\[ E = 2G\left( {1 + \nu } \right) \]

We obtained the relation between Young’s modulus \( E \) and shear modulus \( G \).

We can also relate the bulk modulus \( K \) to Young’s modulus \( E \). Consider a hydrostatic stress state acting on an isotropic cube shown below.

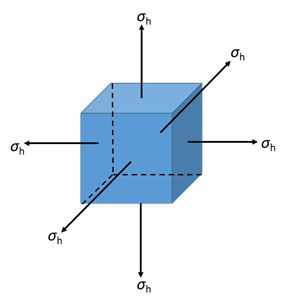
isotropic cube diagram

By the principle of superposition, the linear strain in each orthogonal direction is

\[ {\varepsilon_x} = {\varepsilon_y} = {\varepsilon_z} = \frac{{{\sigma _h}}}{E} - \nu \frac{{{\sigma _h}}}{E} - \nu \frac{{{\sigma _h}}}{E} = \frac{{{\sigma _h}}}{E}\left( {1 - 2\nu } \right) \]

The volumetric strain \( \Delta \) is

\[ \Delta = { \varepsilon_x} + {\varepsilon_y} + {\varepsilon_z}= 3\frac{{{\sigma _h}}}{E}\left( {1 - 2\nu } \right) \]

The proof of the first line can be found in here.

From the definition of bulk modulus,

\[ K = \frac{{{\sigma _h}}}{{\rm{\Delta }}} \]

And equating the volumetric strain \( \Delta \), gives the relation between Young’s modulus E and bulk modulus K:

\[ \frac{{{\sigma _h}}}{K} = 3\frac{{{\sigma _h}}}{E}\left( {1 - 2\nu } \right) \]

\[ E = 3K\left( {1 - 2\nu } \right) \]

Equating the two expressions for Young’s modulus, \( E \) yields a relationship between \( G \) and \( K \),

\[ 2G\left( {1 + \nu } \right) = 3K\left( {1 - 2\nu } \right) \]

Interestingly, for an isotropic material, if two of the four elastic constants, \( E \), \( G \), \( K \), \( \nu\) are known, the others can be calculated.

PreviousNext